数学-机器学习-降维

五 降维

5.1 简介

降维-思维导图

5.2 内容

5.2.1 背景

前期提到，解决过拟合，有三种方法

1. 增加样本数
2. 正则化：限制参数空间，给他一些约束。这样在求参数x的矩阵一定可逆
3. 降维

这里我们重点就是降维，降维分为三种方式

1. 直接降维：特征选择
2. 线性降维：PCA、MDS
3. 非线性降维：流形:LLE(局部线性嵌入),ISOMAP(等度量映射)

引出降维的方法以后，我们再说一下降维是怎么来的，降维的思路来源于维度灾难(dimensial cruse)的问题，维度灾难是什么呢：
随着维度的增加，数据会出现维度灾难，数据会十分稀疏。几何表现上就是数据都不会位于球内，而是都集中在正方体和球之间，如下图。

在高维数据中，主要样本都位于立方体的边缘，数据集更加稀疏。

5.2.2 样本均值&样本方差矩阵

背景

为了方便，我们首先将协方差矩阵（数据集）写成中心化的形式，中心化是啥：

它的意义就是把数据归零化，将数据点往原点附近拉，如下图。每一维减去它的均值就能实现。

A 已知

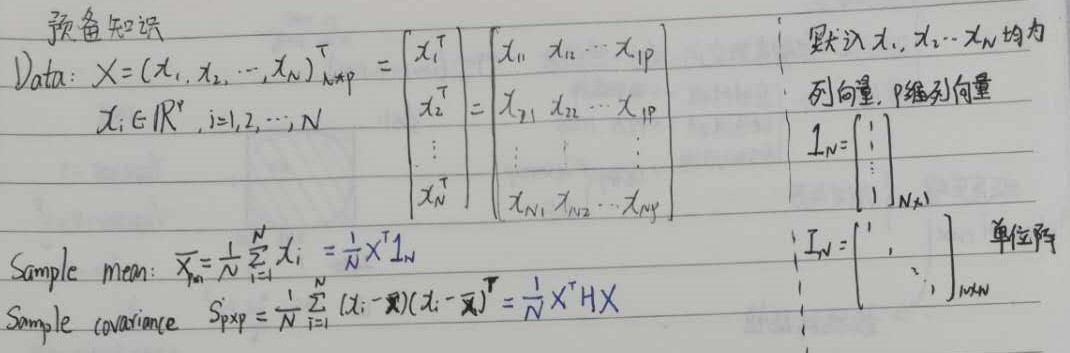
B 求

样本均值$\bar X$

样本协方差$\bar S$

C 解

样本均值

$$\begin{align} \bar X = \frac{1}{N}\sum\limits_{i = 1}^N { {x_i}} = \frac{1}{N}\left( {\begin{array}{*{20}{c}} { {x_1}}&{ {x_2}}& \ldots &{ {x_N}} \end{array}} \right){\left( {\begin{array}{*{20}{c}} 1\\ 1\\ \vdots \\ 1 \end{array}} \right)_{N \times 1}} = \frac{1}{N}{X^T}{1_N} \end{align}$$

样本协方差

H为centering matrix，中心化矩阵

$$\begin{align}S&=\frac{1}{N}\sum\limits_{i=1}^N(x_i-\overline{x})(x_i-\overline{x})^T\nonumber\\ &=\frac{1}{N}(x_1-\overline{x},x_2-\overline{x},\cdots,x_N-\overline{x})(x_1-\overline{x},x_2-\overline{x},\cdots,x_N-\overline{x})^T\nonumber\\ &=\frac{1}{N}(X^T-\frac{1}{N}X^T\mathbb{I}_{N1}\mathbb{I}_{N1}^T)(X^T-\frac{1}{N}X^T\mathbb{I}_{N1}\mathbb{I}_{N1}^T)^T\nonumber\\ &=\frac{1}{N}X^T(E_N-\frac{1}{N}\mathbb{I}_{N1}\mathbb{I}_{1N})(E_N-\frac{1}{N}\mathbb{I}_{N1}\mathbb{I}_{1N})^TX\nonumber\\ &=\frac{1}{N}X^TH_NH_N^TX\nonumber\\ &=\frac{1}{N}X^TH_NH_NX=\frac{1}{N}X^THX \end{align}$$

D 手稿

5.2.3 最大投影方差

背景

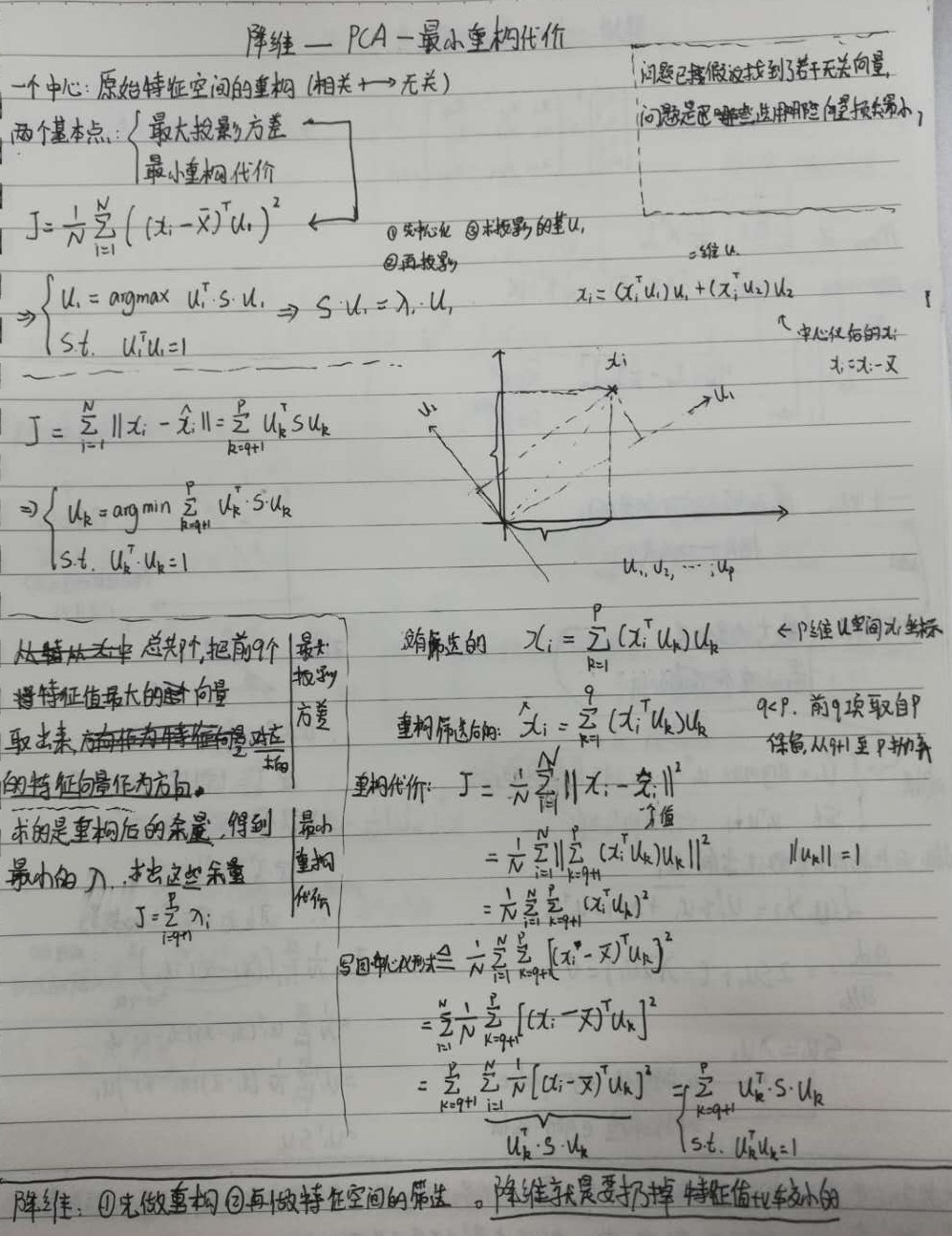
一个中心：原始特征空间的重构（相关->无关）

两个基本点：最大投影方差、最小重构代价。这两个是一个意思，两种角度。

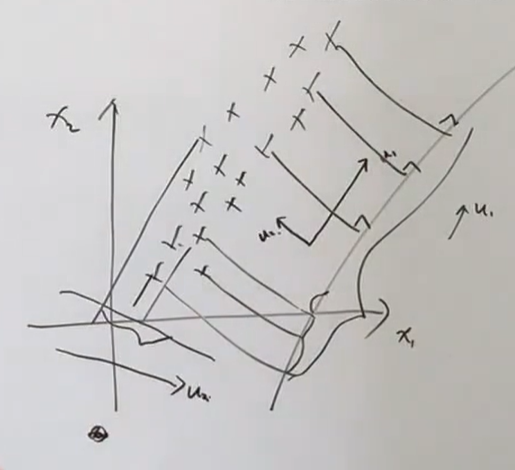
要让它投影到$u_1 , u_2$分布的互相更远，即方差最大，距离最远。如果不远，都堆一起了，就无法最大程度还原原始数据。

两个基本点服务于一个中心。

A 已知

B 求

B.1 投影方差

B.2 建模

$$\begin{align} \left\{ {\begin{array}{*{20}{l}} { { {\hat u}_1} = \arg \max u_1^T \cdot S \cdot {u_1}}\\ {s.t.\begin{array}{*{20}{c}} {}&{u_1^T{u_1} = 1} \end{array}} \end{array}} \right. \end{align}$$

C 解

D 收获

最大投影方差，最小重构距离，其实就是一个意思的两种不同表达，要让它投影到(u1、u2)后样本点们离的越远越好，即样本点们方差最大，距离最远。

如果不远，都聚集在一起，就无法最大程度还原原始数据。

5.2.4 最小重构代价

A 已知

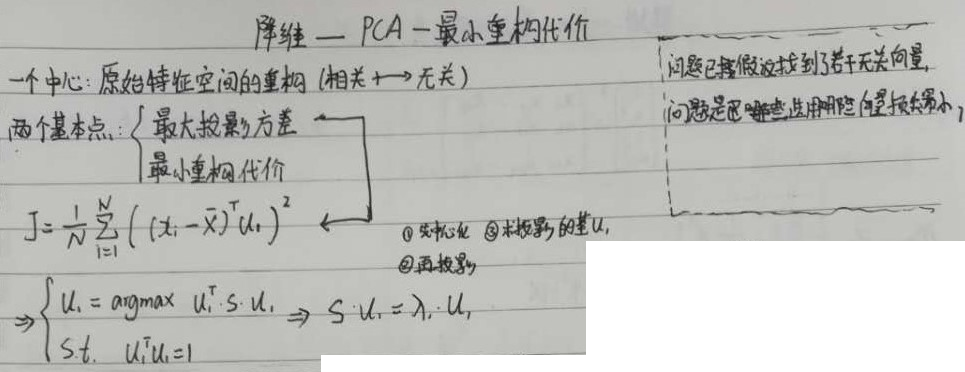
B 求

最小重构代价损失函数及建模

C 解

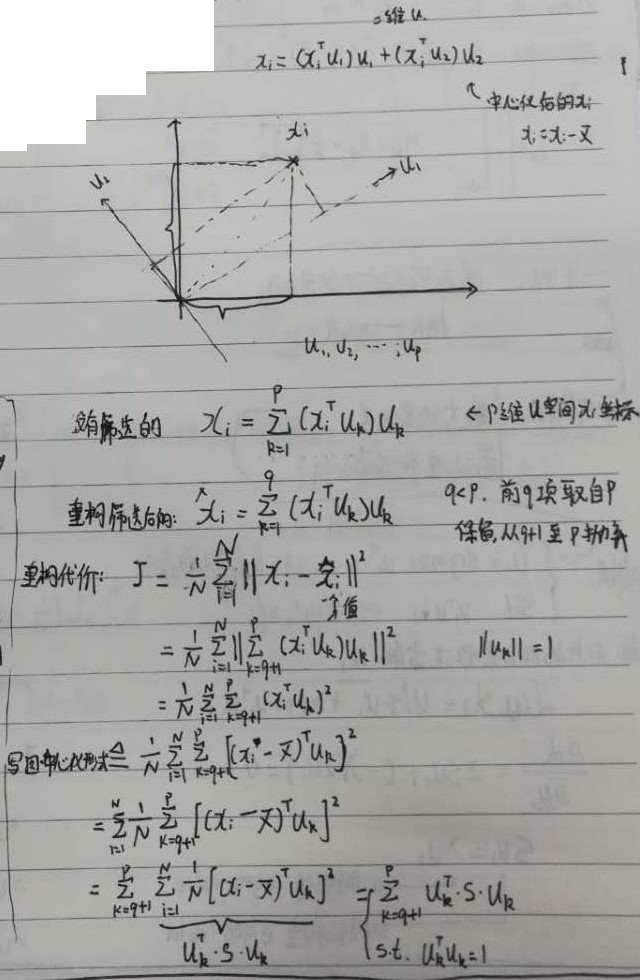
D 收获

降维过程：

1. 先做重构
2. 再做特征空间的筛选。扔掉特征值比较小的。

最大投影方差：

 总共p个，把前q个特征值最大的向量取出来，对应的特征向量作为方向

最小重构代价：

 求的是重构后的余量，得到最小的$\lambda $，求出这些余量$J = \sum\limits_{i = q + 1}^p { {\lambda _i}}$

E 手稿

5.2.5 SVD角度看PCA和PCoA

A 已知

B 分析

5.2.6 主成分分析(PCA)-概率角度(Probabilistic PCA)

背景

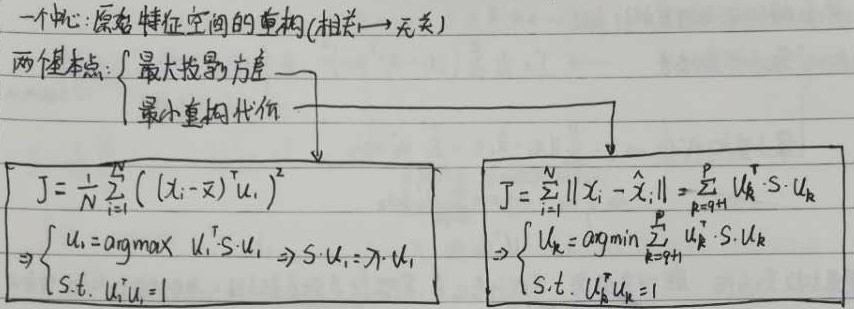
一个中心：原始特征空间的重构(相关->无关)

两个基本点：最大投影方差、最小重构代价

A 分析

5.3 问题

5.4 小结

降维的过程：1）先做重构；2）再做特征空间的筛选。降维就是要扔掉特征值比较小的。

以下来自tsyw的github库笔记

降维是解决维度灾难和过拟合的重要方法，除了直接的特征选择外，我们还可以采用算法的途径对特征进行筛选，线性的降维方法以 PCA 为代表，在 PCA 中，我们只要直接对数据矩阵进行中心化然后求奇异值分解或者对数据的协方差矩阵进行分解就可以得到其主要维度。非线性学习的方法如流形学习将投影面从平面改为超曲面。

参考文献

[1] shuhuai008. 【机器学习】【白板推导系列】【合集 1～23】. bilibili. 2019.
https://www.bilibili.com/video/BV1aE411o7qd?p=13

[2] tsyw. https://github.com/tsyw/MachineLearningNotes