最大似然估计MLE和最大后验估计MAP

一 前言

小伙为何会提出两个单词MLE和MAP呢。竟然是因为这….

好吧，是因为不知道为何搞不懂这两个名词的意思。最早听到最大似然估计MLE是在考研数学里面，有一道概率题，要求一组数据的最大似然估计，然后强行记住了求法，具体的求法就是，现在也记不清了，讲个大概流程：

1. 先把题目给的那组数中，每个数出现的概率和它们自己相乘，求出似然函数L(θ)
2. 然后加个log运算，变成log(L(θ))
3. 然后就是求导，令求导结果为0
4. 解出想要的参数θ

这才讲到MLE的疑问来源，那么，MAP又是怎么相识的呢，说到这个MAP，我们好像在哪见过，我不记得了，记得那是一个前几个月的日子，我看机器学习视频的时候，老师讲到

贝叶斯派，要用MAP求出想要的参数θ

于是，MLE和MAP就这么进入了小伙的生活，并开始了一段迷茫的日子。时至今日，小伙在总结学习笔记的时候，她们就这么生生的又来了。小伙决定，写个文档，记录一下。

二 MLE

2.1 简介

极大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或最大似然估计，是求估计的另一种方法，最大概似是1821年首先由德国数学家高斯（C. F. Gauss）提出，但是这个方法通常被归功于英国的统计学家。罗纳德·费希尔（R. A. Fisher）

2.2 用途

用于求解未知常数参数θ，使得$logP(X|\theta)$取得最大值。式子为

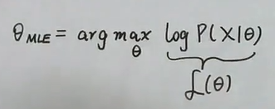
最大似然估计就是求使$L(\theta )$最大的$\theta$是多少，具体方法就是利用求导的方法：

$$\frac{ {\partial L(\theta )}}{ {\partial \theta }} = 0$$

至于为什么加上log，因为一般$P(X|\theta)$是一个乘积的形式，加上log后，就可以变成累加的形式，简化计算。

三 MAP

3.1 简介

最大后验估计（maximum a posteriori probability estimate, 简称MAP）。

3.2 用途

MAP常用于从贝叶斯角度估计求参数$\theta$。

在贝叶斯角度下，参数$\theta$不再是一个常数，贝叶斯派设置的参数$\theta$是一个概率分布，它是有先验知识p(θ)的，并不像是频率派参数$\theta$是一个常数。贝叶斯派想要求出使得概率值最大的$\theta$，就需要借助贝叶斯公式进行硬算，在硬算的过程中，需要借助$\theta$的先验知识。最后要求得的那个概率值就是一个后验概率，那个后验概率是$P(\theta|y)$

MAP:

$${\theta _{MAX}} = \mathop {\arg \max }\limits_\theta P(\theta |y)$$

而这个后验概率$P(\theta|y)$，需要通过贝叶斯公式来求：

$$P(\theta |y) = \frac{ {P(y|\theta )P(\theta )}}{ {P(y)}}$$

在这里，p(θ)是先验，是已知的，p(y|θ)也是可以求得的，p(y)是样本概率，是常量。然后MAP就能算出来了。

3.3 举个栗子：

从贝叶斯角度看岭回归的最大后验估计。栗子的目的就是看一看MAP求解过程。

A 已知

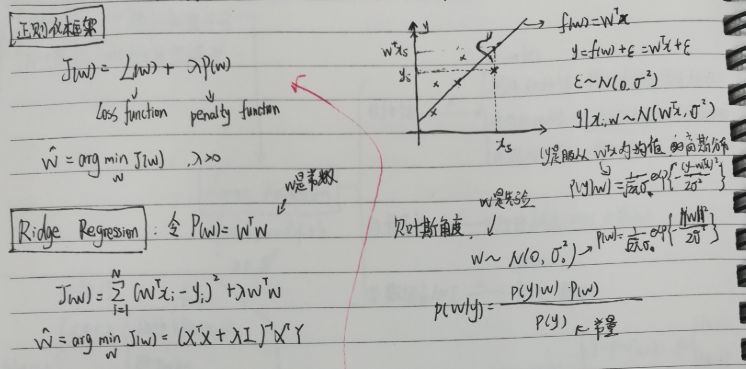
B 求

参数w的最大后验估计MAP。

C 解

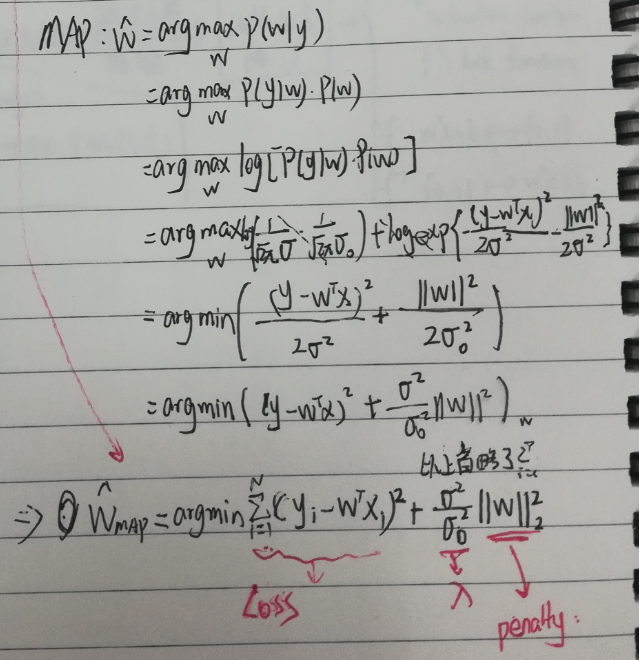
四 MLE和MAP的相爱相杀

• MLE是概率角度求解未知常数参数θ
• MAP是贝叶斯角度求解未知概率分布参数θ

  参考资料

  [1] https://blog.csdn.net/liangjiubujiu/article/details/84871196
  [2] 百科百科. 极大似然估计. https://baike.baidu.com/item/%E6%9E%81%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1/3350286?fr=aladdin
  [3] shuhuai008. 【机器学习】【白板推导系列】【合集 1～23】. bilibili. 2019.
  https://www.bilibili.com/video/BV1aE411o7qd?p=9