数学-机器学习-线性回归

三 线性回归

Linear Regression

3.1 思维导图简述

线性回归-思维导图

3.2 内容

3.2.1 最小二乘法及其几何意义

背景

最小二乘法LSM(Least Squre Method)，表面意思就是让二乘得到的结果最小，二乘又是什么呢，二乘就是两个数相乘，也就是平方，那么我们就可以轻松的得到最小二乘法的Loss Function：

$$L(w) = \sum\limits_{i = 1}^N { { {\left( { {w^T}{x_i} - {y_i}} \right)}^2}}$$

A 已知

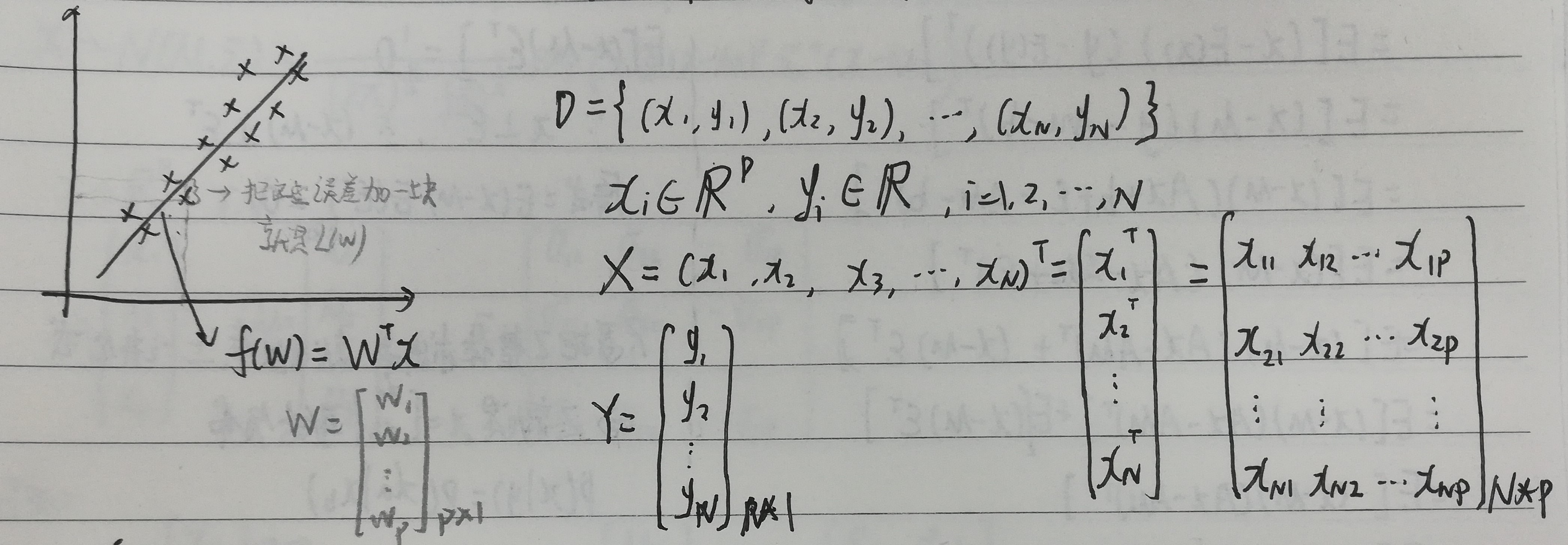
B 求

令L(w)最小的w是多少。

C 解

最后求得的结果是$w=(X^{T}X)^{-1}X^{T}Y$。

其中，${({X^T}X)^{ - 1}}{X^T}$又称为伪逆。

这里存在$(X^{T}X)^{-1}$中的$X^{T}X$不一定可逆的问题。

D 收获

最小二乘法的几何意义有两个：

1. 在下图中，最小二乘法就是将所有的实际值-估计值误差都累加起来.

   把误差分成了n段

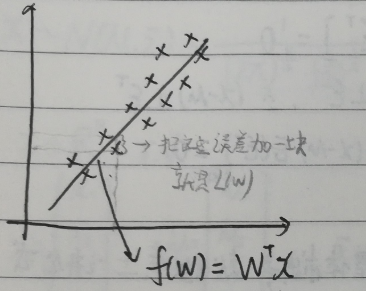
1. 高维空间的投影

   把误差分散在n个维度里面

X是N*P维矩阵，按列选取p维，构成p维的子空间

把$f$写成$x^{T}\beta$的形式。然后$f(w)=w^{T}x=x^{T}\beta$不在p维子空间里，因为除非n个样本点都在回归曲线上，才可能出现$f(w)$在p维子空间中。

我们要求的最小二乘法从几何意义上表述就是，向量$Y$在p维空间中找一条线，让$Y$离这条线最近，或者说向量$Y$离这个平面最近，很显然就是$Y$的投影。而这个投影就是$x_1, x_2, ..., x_p$的线性组合。

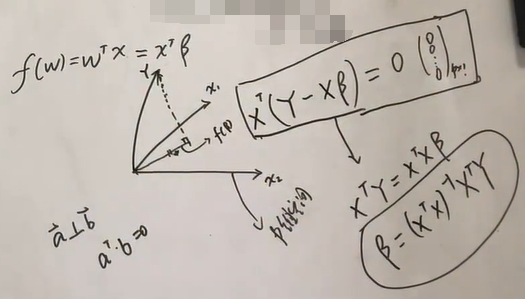
法向量可以表示为$(Y-X\beta)$

法向量肯定垂直于p维空间，所以$X^{T}(Y-X\beta)=0$，求解得出$\beta=(X^{T}X)^{-1}X^{T}Y$

3.2.2 最小二乘法-概率视角-高斯噪声-MLE

背景

从概率角度看最小二乘法，实际上就是用概率分布函数PDF来硬算，这个PDF要是高斯噪声才可以让最大似然估计=最小二乘估计的结果。MLE=LSE

A 已知

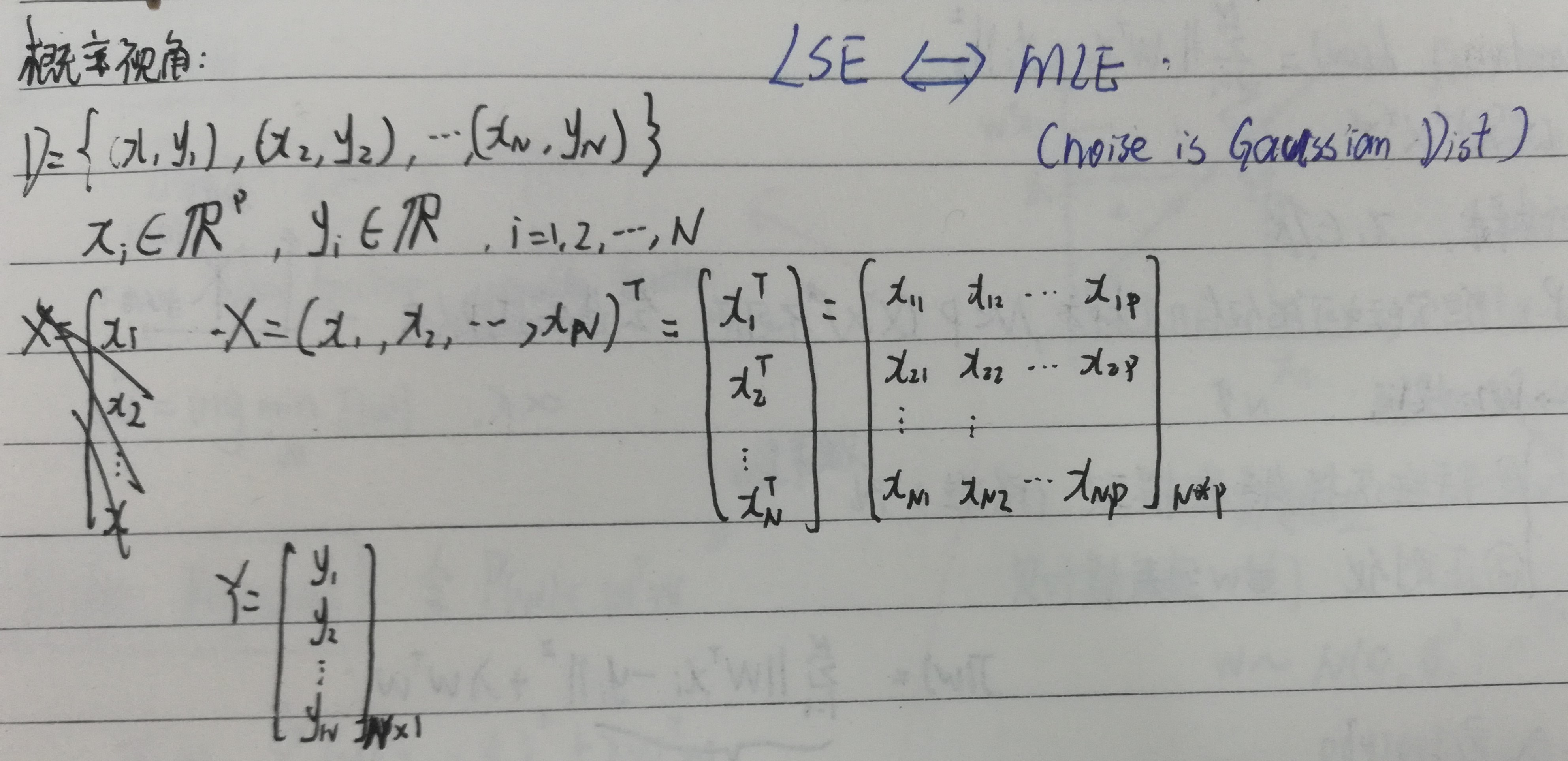
B 求

假设$p(Y|x_i,w)$的概率密度函数是一维高斯分布函数，服从的高斯分布均值为$w^{T}x$，方差为$\sigma^2$。求参数w的MLE。损失函数定义为：

$$L(w) = logP(Y|{X_i},w)$$

C 解

当$P(Y|x_i,w)$服从正态分布，才有MLE=LSE，最小二乘法估计定义为$L(w) = \sum\limits_{i = 1}^N {\left\| { {w^T}{x_i} - y} \right\|_2^2}$

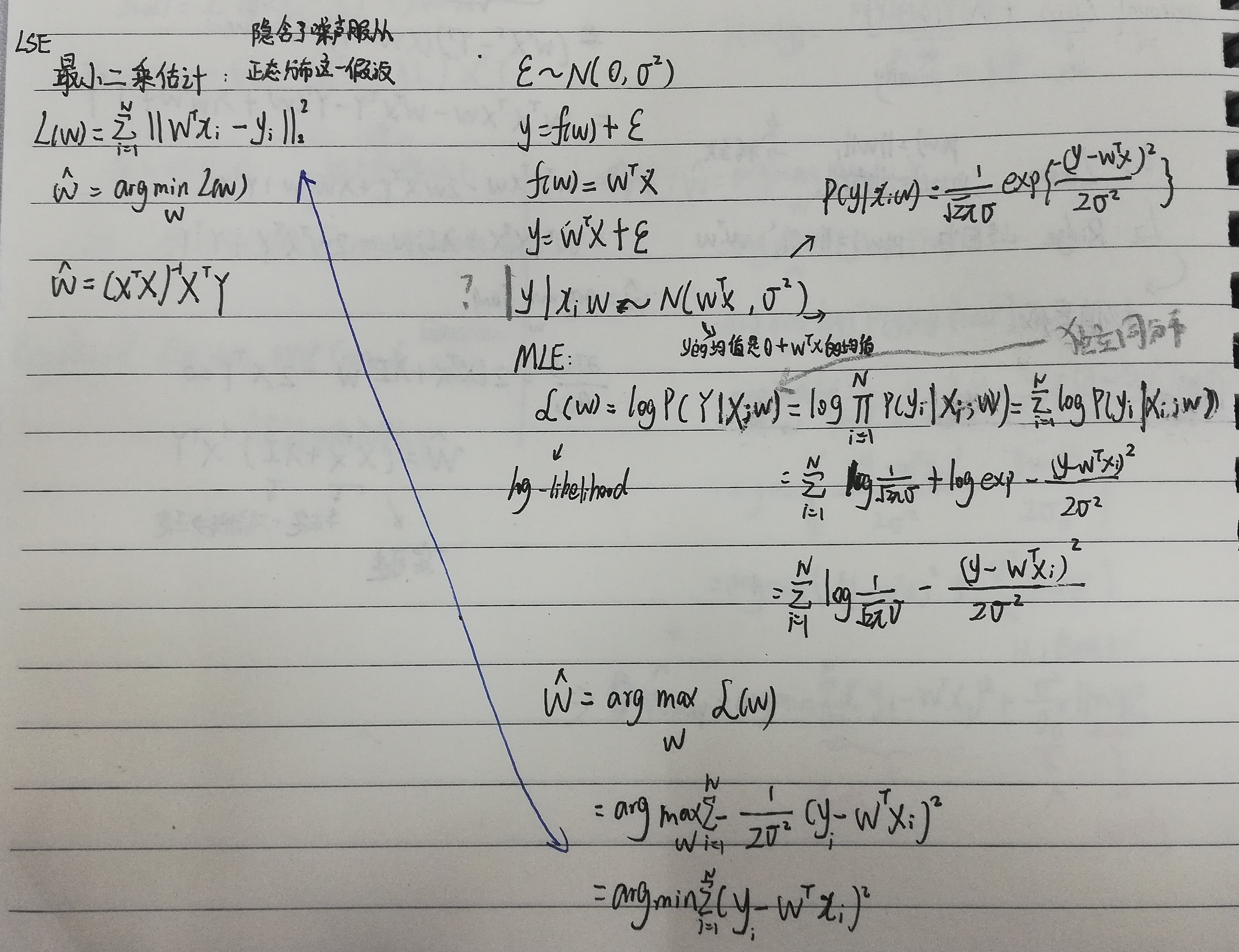
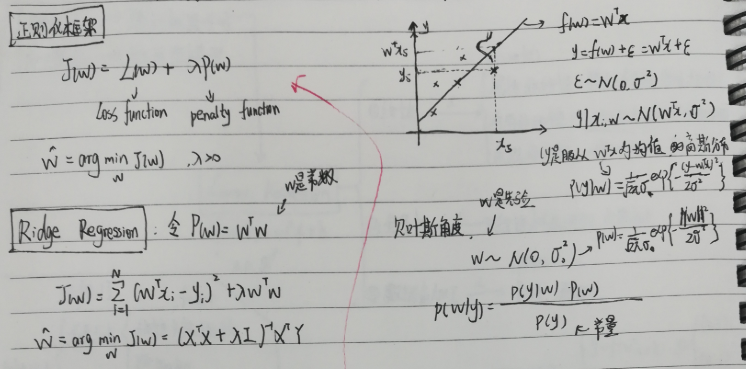
3.2.3 正则化-岭回归-频率角度

Regularization - Ridge Regression - Bayesians

背景

正则化是为了解决过拟合问题而提出的。regularization，让它正常，不要那么不正常了，那么这个不正常体现在那里呢，目前[2020-5-15]来看，不就是它过拟合了，不像正常的那样了。

过拟合是什么呢？
过拟合从字面意义上看，就是拟合过度了，什么才叫拟合过度呢？看下图。一个点，有好多情况，你得到的曲线，只适合某一种样本点，其他样本点适应性极差。

• 从数据角度分析：首先，$X$是样本数据阵，它是一个N*P维的矩阵，N表示的样本的数量，P维表示的是每一个样本的状态数，就是N个样本，每个样本是p维的。然后，理论上应该样本数N应该远大于样本的维数P，但是，实际中可能仅有几个样本，出现N<P的情况，那么就会造成过拟合
• 从数学角度分析：在3.2.1中得到的$(X^{T}X)^{-1}$中的$X^{T}X$不可逆，就会直接造成过拟合。

解决过拟合的方法：

• 增加样本数量
• 特征选择/特征提取，实际就是降维，降低p的维数。PCA
• 正则化，对w约束，改变w的形式，把$(X^{T}X)^{-1}$改造成一个绝对可逆的式子。

正则化分为两种

1. L1 -> Lasso
2. L2 -> Ridge

A 已知

B 求

正则化下，新的w形式

C 解

$$\hat w = {({X^T}X + \lambda I)^{ - 1}}{X^T}Y$$

D 收获

正则化：解决过拟合问题。过拟合由$\hat w = {({X^T}X)^{ - 1}}{X^T}Y$中${({X^T}X)^{ - 1}}$不可逆引起。正则化就是构造新Loss Function J(w)，推出的$\hat w$就是可逆的，且一定可逆，将不可逆变成可逆。

3.2.4 正则化-岭回归-贝叶斯角度

A 已知

B 求

参数w的最大后验估计MAP。

C 解

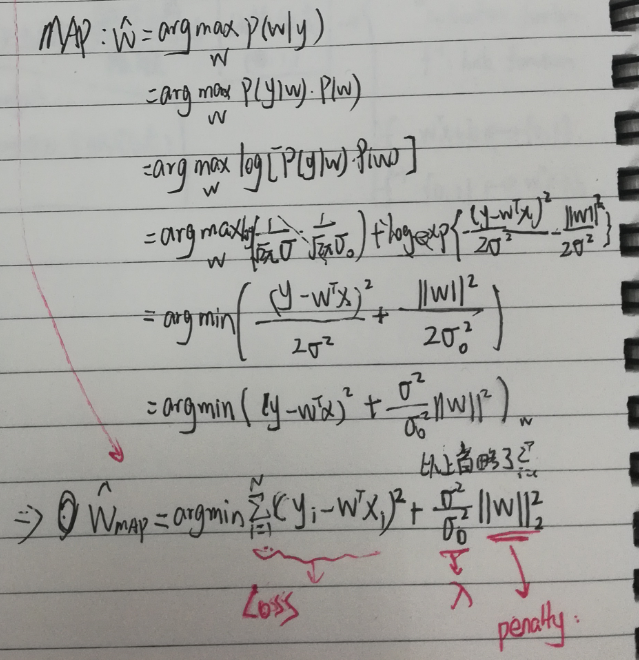
D 收获

从贝叶斯角度用最大后验概率估计进行分析，惊人的发现，在参数w先验知识是高斯分布的情况下，居然和正则化的最小二乘估计是一样的

3.3 问题

3.3.1 为什么贝叶斯角度分析求的就是最大后验估计MAP呢

因为贝叶斯派设置的参数w是一个概率分布，它是有先验知识的，并不像是频率派参数w是一个常数。贝叶斯派想要求出使得概率值最大的w，就需要借助贝叶斯公式进行硬算，在硬算的过程中，需要借助w的先验知识。最后要求得的那个概率值就是一个后验概率，在3.2.4中，那个后验概率是$P(w|y)$

3.3.2 正则化(regularized)是什么

将不可逆变为可逆即为正则化

为什么需要正则化，首先正则化出现的背景是最小二乘法$w=(X^TX)^{-1}X^TY$中式子$X^TX$可能是不可逆的，从数学角度分析就是X为N*p维的矩阵，N表示样本数，p是Xi的状态向量数，在实际应用中，可能测得的样本数很少，出现了N<P的情况，即$X^TX$不可逆，那么w就求不来。

这样不可逆会导致什么后果呢。答，会引起过拟合。因为如果样本数过少，那么拟合的方法就会有很多。出现错误的几率就会很高。

怎么解决这个问题提，答，引入正则化。正则化实际上就是给最小二乘法的损失函数(Loss Function)L(w)加一个框架，得到一个新的函数J(w)，其中$J(w)=L(w)+\lambda P(w)$。这样求出的w就会绝对可逆。

3.3.3 最小二乘法的第二个几何意义

真实空间是x1, x2, …, xn，测量值y没有在真实空间中，y的估计值在真实空间里最接近的那个就是它在真实空间的投影$f(w)=x^{T}β$，其中真实空间x与这个投影f(w)是垂直的。所以就有$X^{T}(Y-Xβ)=0$，解出β就是所求的最小二乘法得出的最优w

• 不知道为什么$f(w)=x^{T}β$，这个β是什么，这个β也是类似于w的参数，那条投影在真实空间中的表示就是用$x^{T}β$来表示。要求的也是这个β。（不同的β，Xβ表示真实空间不同的对象）
• Y-Xβ，完全是为了等式成立才这么写，这个量表示的是那条垂直的虚线，垂直的虚线和真实空间垂直，所有有了$X^{T}(Y-Xβ)=0$

3.3.4 矩阵求导规则

推荐，哈工大严质彬，矩阵论

公式查询: 矩阵求导法则与性质

参考文献

[1] shuhuai008. 【机器学习】【白板推导系列】【合集 1～23】. bilibili. 2019.
https://www.bilibili.com/video/BV1aE411o7qd?p=9

[2] 3.2.4 正则化-岭回归-贝叶斯角度手稿

[3] zealscott. 矩阵求导法则与性质. CSDN. 2018. https://blog.csdn.net/crazy_scott/article/details/80557814