一绪论

1.1 思维导图简述

机器学习思维导图

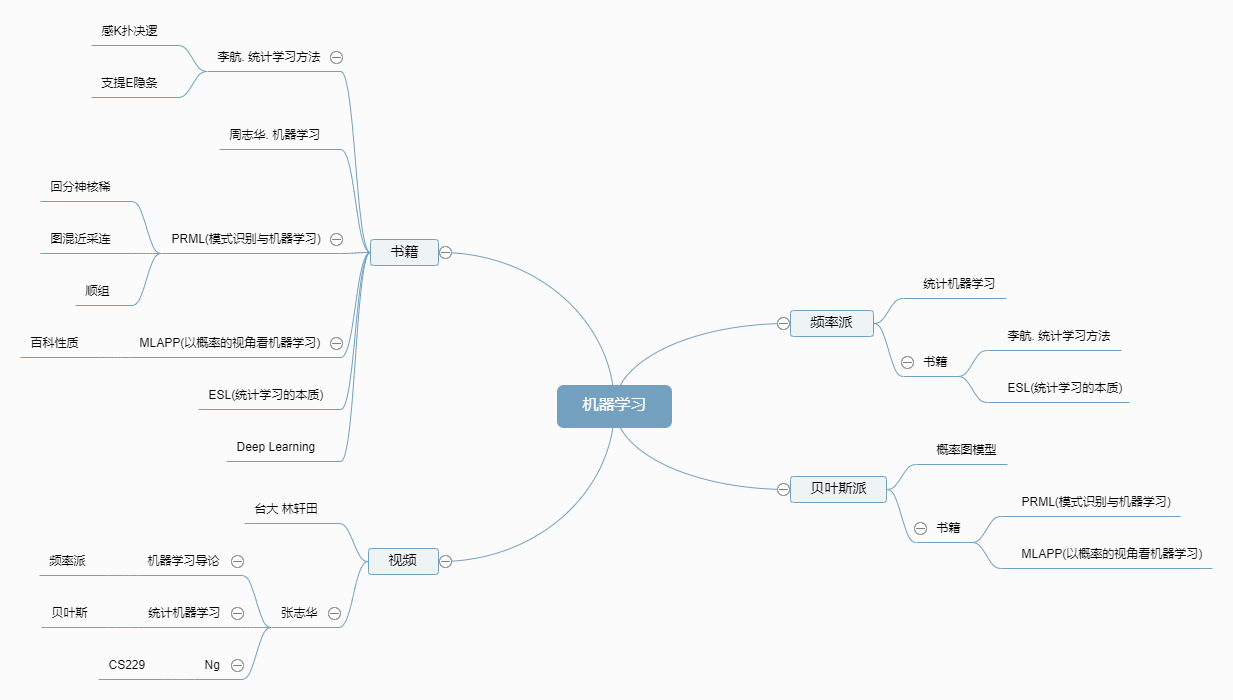
1.2 频率派Vs贝叶斯派

区别

频率派，参数θ是常数，只不过它未知。贝叶斯派，参数θ是一个概率分布，它有先验知识 $\theta \sim p(θ)$

频率派是统计机器学习方法，就其本质而言，是一个优化问题。即将问题分为三步走：

建立模型
设计Loss Function
algorithm

贝叶斯派则是概率图模型，就其本质而言，是求积分的问题。而其中最常用的就是MonteCarlo Method

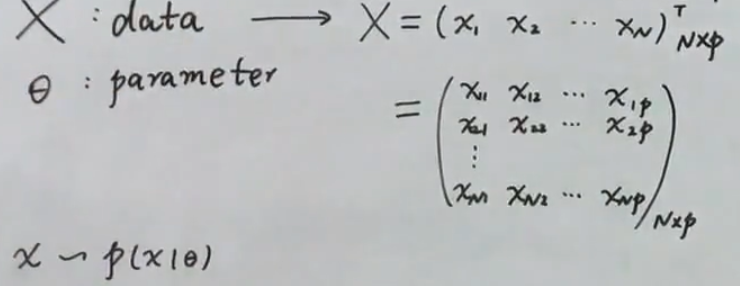
A 频率派：

θ是一个未知的常量，X是随机变量，它更关心是数据，它要做的就是把θ估计出来，最常用的方法就是最大似然估计MLE(Maximum likelihood estimation)

MLE

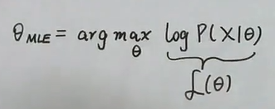
最大似然估计就是求使 $L(\theta )$ 最大的 $\theta$ 是多少，具体方法就是利用求导的方法：

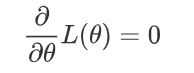
至于为什么加上log，因为一般 $P(X|\theta)$ 是一个乘积的形式，加上log后，就可以变成累加的形式，简化计算。

B 贝叶斯派

与频率派不相同的是，贝叶斯派认为θ不是一个常量，它是一个概率分布，它有一个先验知识。而后借用贝叶斯定理把参数的先验和后验用似然联系起来。利用MAP(Maximum a posteriori estimation)最大后验估计来求出参数θ。

其中，P(X)是一个常量与θ没有关系，就是一个积分常量，因而可以写成正比于 $\int {P(X|\theta )} P(\theta )d\theta$ 。

MAP

MAP是最大后验估计，就和其含义一样，它的目的是使后验概率最大。参数θ是一个概率分布，要找到一个使得后验概率最大的那个点，来代替它的估计。这个点是众数的概念。

最大后验估计MAP，其和最大似然估计MLE不同的是：

在MLE中，参数θ是一个定值，只是这个值未知，最大似然函数是θ的函数，这里的θ是没有概率意义的，但是，在MAP中，θ是有概率意义的，θ有自己的分布，而这个分布函数，需要通过已有的样本集合X得到，即最大后验估计MAP需要计算的是 $p(\theta|X)$

MAP并不是严格意义上的贝叶斯估计。真正的贝叶斯估计就是要实打实的求这个积分 $\int {P(X|\theta )} P(\theta )d\theta$ ，而后求出后验概率。求出的这个后验概率能干嘛呢？就可以引出贝叶斯预测。
实际上在整个参数空间求积分是很困难的，所以从贝叶斯角度发展出来很多解析方法，概率图模型。实际上贝叶斯就是求积分，解析解求不出来，我们还可以用MonteCarlo Method

1.3 问题

Q1: 什么是机器学习

机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。

Q2: 说的频率派和贝叶斯派为什么看起来和想的机器学习不一样

现在分析的是数学理论，是数学描述方法，你想的是应用层次问题，应用层次的底层才是机器学习数学理论。总结就是，急啥急，边走边看。

参考资料

[1]shuhuai008. 【机器学习】【白板推导系列】【合集 1～23】. bilibili. 2019.
https://www.bilibili.com/video/BV1aE411o7qd?p=1

[2] zhaosarsa. 【数学基础】参数估计之最大后验估计（Maximum A Posteriori，MAP）. CSDN博客. 2018.
https://blog.csdn.net/qq_32742009/article/details/81477611

[3] 笔记手稿.

AYZP

数学-机器学习-绪论

一绪论

1.1 思维导图简述

1.2 频率派Vs贝叶斯派