时间复杂度logn怎么来的啊

前言

以前一直疑惑为什么算法复杂度会蹦出一个$nlog(n)$出来，怎么会有这个东东啊。然后今天，我看到我二分法的笔记，又来了算法复杂度$nlog(n)$，于是我迈出了我学习的第一步，我决定去搞懂它。

一 提出问题

// 迭代
int binary_search(int a[], int n, int x)
{
	int left, right, mid;
    left = 0; right = n-1;	//确定查找段的起点和终点
    while (left <= right)
    {
        mid = (left + right) / 2;
        if (x == a[mid]) return mid; //查找到，返回
        if (x < a[mid]) right = mid - 1; //左端查找
        else left = mid + 1; //右端查找
    }
    return -1;
}

很显然，这是一个二分法的程序，一次执行的算法复杂度是$log(n)$，n次执行的算法复杂度是$nlog(n)$，那么这个$log(n)$老人家是怎么来的呢？

二 分析问题

经过百度，我找到了一个答案，很好理解，我直接盗图，文章来源见参考文献[1]。

那么看到这里其实，答案就有了嘛，因为这就是个数学问题吗，当执行一次该程序，循环次数i趋于无穷，复杂度不就是log(n)，这里的log其实是$log{e}n$，其他地方的log可能是$log{2}n$呢。

三 解决问题

那么明白了什么情况是$O(log(n))$，那么二分法的复杂度是怎么计算出来的呢：

四 拓展

算法复杂度大家庭，一家人就要整整齐齐的。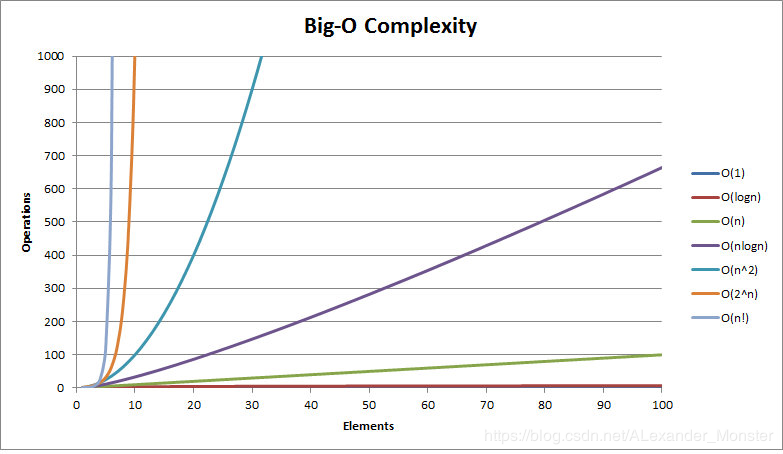

【图片来自】

O(1)<O(logn)<O(n)<O(nlogn)<O(n^2^)<O(2^n^)<O(n!)

参考文献

[1] shikelang_pp. 算法复杂度O(nlogn)详解. CSDN博客. 2017. https://blog.csdn.net/shikelang_pp/article/details/77145684
[2] Martini. 算法复杂度速查表. 博客园. 2019. https://www.cnblogs.com/martini-d/p/fu-za-du.html